Abstracts

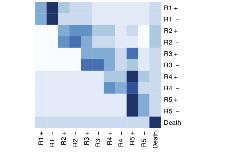
Rationale: Antiepileptic drug therapy constitutes first line treatment for epilepsy management. However, the long-term outcomes of antiepileptic drug therapy are poorly understood, hampering the selection of a rational and effective management plan. We performed mathematical modelling to investigate the patterns and trends of treatment outcome, that might not otherwise be obvious intuitively, or using standard statistical methods. Methods: Multi-state and Markov models have been successfully used in analysing the progression of stages of disease in other specialties, such as chronic kidney disease and diabetic retinopathy. We applied this methodology to disease progression in epilepsy, by applying it to longitudinal data from our previous observational study of 1795 patients (969, 54% male; median age 33 years, range 9-93) with newly diagnosed epilepsy. These patients were managed in real-world clinical setting and prospectively followed for up to 30 years (median 11 years, interquartile range: 7-16). We created a framework for conceptualising the natural history of epilepsy as a step-wise progression of disease through various stages, using antiepileptic regimen as a proxy for disease severity/chronicity, and the presence or absence of seizure freedom. We formulated a multi-state Markov model based on the framework, and analysed it standard statistical methods. Fig. 1: Schematic of the Markow model. States reflect increasing anti-epileptic drug regimen, and the presence or absence of seizure freedom. The absorbing state is death. Transition probabilities (p_i,j) label allowed transitions of the model, from state i to state j. Results: We generated transition probabilities for the model, representing the dynamics of moving between disease states, and probability of being seizure free. We show that at all stages of epilepsy, achieving seizure freedom confers a lasting benefit in terms of longer term seizure freedom. The generated transition probabilities could also form the basis of clinical prognostication and decision making tools. Fig. 2: A heatmap summarising the 5 year transition probabilities of seizure freedom from each state (that is, beginning at a certain state, what is the 5 year probability of seizure freedom). R1 = regimen 1, R2 = regimen 2, etc. A '+' sign indicates seizure freedom, while a '-' sign indicates absence of seizure freedom. Seizure freedom defined as being seizure free for 6 months in the model.We further analysed the dynamics of epilepsy progression, by calculating survival probabilities from each state, as well as average and total time spent in each state. We found that patients on lower anti-epileptic drug regimens, spent more time seizure-free than those on higher regimens, and were able to quantify this  relationship. Conclusions: Epilepsy can be conceptualised as multi-stage, stepwise disease process, using anti-epileptic drug regimen as a proxy for disease progression. Markov and multi-state models can be used to model the natural history of epilepsy in this way, and inform us of the likely patterns and outcomes of epilepsy at the various stages in its progression. This quantification of outcomes can help us better inform patients of their prognosis at various stages in their illness. This information can also potentially inform us when to intervene earlier with non-pharmacological and advanced therapies, in patients with a worse prognosis. Funding: Not applicable